gnuplotで正規乱数を発生させて、gnuplotでそのヒストグラムを作成
gnuplotのちょっとアクロバティックな使い方と簡単な統計の取り方、確率密度分布の作り方を説明します。ちょっとしたデータ解析はgnuplotで、お手ものもの。
gnuplotで正規分布に従う乱数を作成する方法
gnuplotには、の範囲で一様乱数を出力する組み込み関数がある。これをBox-Muller法で変換することで正規分布に従う疑似乱数を作る。書き出し先は、適当に、data.datというファイルにしておく。
| set print "data.dat"
do for [i=1:1000]{print i, sqrt(-2*log(rand(0)))*cos(2*pi*rand(0))}
|
| 1 1.17899556743398
2 1.18496843008846
3 0.131057381960924
4 1.47129343802476
5 1.58966104438536
6 0.521011248122543
7 -0.088706223302425
8 -0.322006285605902
9 -0.0312462476923427
10 0.824071844023501
|
乱数列の解析1:平均値と分散の取得
出力先を標準出力に戻して、statsコマンドを利用することで、平均値や分散などを取得可能。
| set print "-"
stats "data.dat"
|
出力結果は下記のようなもの。
項目の意味の詳細は、https://ss.scphys.kyoto-u.ac.jp/person/yonezawa/contents/program/gnuplot/stats.htmlなどのサイトやhelp stats、公式ドキュメントなどを参照してください。
ここでは、カラム欄の2番目の項目を見る。正規乱数であるから、平均値が0.0385とおおよそ0であり、標準偏差が0.9790とおおよそ1であることが確認できる。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34 | * FILE:
Records: 1000
Out of range: 0
Invalid: 0
Column headers: 0
Blank: 0
Data Blocks: 1
* COLUMNS:
Mean: 500.5000 0.0385
Std Dev: 288.6750 0.9790
Sample StdDev: 288.8194 0.9795
Skewness: 0.0000 0.0059
Kurtosis: 1.8000 2.8365
Avg Dev: 250.0000 0.7935
Sum: 500500.0000 38.4997
Sum Sq.: 3.33834e+08 959.9992
Mean Err.: 9.1287 0.0310
Std Dev Err.: 6.4550 0.0219
Skewness Err.: 0.0775 0.0775
Kurtosis Err.: 0.1549 0.1549
Minimum: 1.0000 [ 0] -2.9571 [ 336]
Maximum: 1000.0000 [ 999] 3.0536 [ 439]
Quartile: 250.5000 -0.6639
Median: 500.5000 0.0354
Quartile: 750.5000 0.7114
Linear Model: y = -0.0001587 x + 0.1179
Slope: -0.0001587 +- 0.0001072
Intercept: 0.1179 +- 0.06196
Correlation: r = -0.04679
Sum xy: 6045
|
乱数の解析2:確率密度分布の作成
gnuplotの本来の機能であるグラフの出力機能を利用しよう。
gnuplotを利用したヒストグラムの作成方法は、
にある。基本的なアイディアはみんな同じだけれども、痒いところに手が届いていない印象。
ここでは、Histogram using gnuplot?の記事の中のものを採用して、
| Min = 0.0
width=0.1
bin(x) = width*(floor((x-Min)/width)+0.5) + Min
|
| plot "data.dat" u (bin($2)):(1.0/width/STATS_records) smooth freq
|
statsを実行した際に設定されている。便利ですねぇ。こうすることで、規格化された確率密度関数をプロットできる。
最期に、少々パラメータを変えつつまとめます。
1
2
3
4
5
6
7
8
9
10
11
12 | # generating data!!
set print "data.dat"
do for [i=1:2000]{print i, sqrt(-2*log(rand(0)))*cos(2*pi*rand(0))}
# analyzing the data
set print "-"
stats "data.dat"
# plot the histogram with the theoretical curve
Min = 0.0; width=0.1; bin(x) = width*(floor((x-Min)/width)+0.5)+Min
plot 1.0/sqrt(2.0*pi)*exp(-x**2/2.0) title "exact",\
"data.dat" u (bin($2)):(1.0/width/STATS_records) smooth freq with line title "data"
|
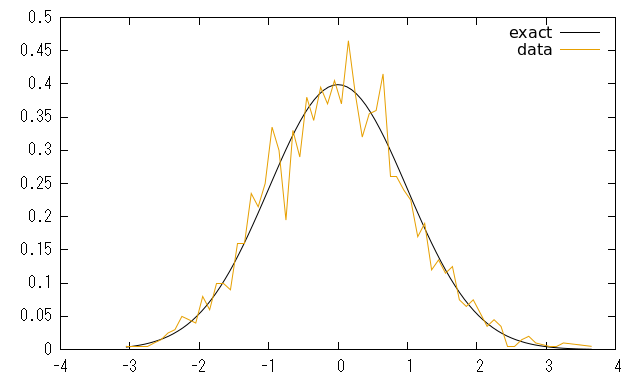
理論と一致したベルカーブが見えました。
